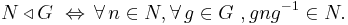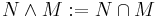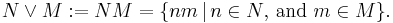Normal subgroup

Concepts in group theory
category of groups
subgroups, normal subgroups
group homomorphisms, kernel, image, quotient
direct product, direct sum
semidirect product, wreath product
Types of groups
simple, finite, infinite
discrete, continuous
multiplicative, additive
cyclic, abelian, dihedral
nilpotent, solvable
list of group theory topics
glossary of group theory

In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group. In other words, a subgroup H of a group G is normal in G if and only if aH=Ha for all a in G.

Évariste Galois was the first to realize the importance of the existence of normal subgroups.

Contents 1 Definitions 2 Examples 3 Properties 3.1 Lattice of normal subgroups 4 Normal subgroups and homomorphisms 5 See also 5.1 Operations taking subgroups to subgroups 5.2 Subgroup properties complementary (or opposite) to normality 5.3 Subgroup properties stronger than normality 5.4 Subgroup properties weaker than normality 5.5 Related notions in algebra 6 References 7 External links

Definitions

A subgroup, N, of a group, G, is called a normal subgroup if it is invariant under conjugation; that is, for each element n in N and each g in G, the element gng⁻¹ is still in N. We write

For any subgroup, the following conditions are equivalent to normality. Therefore any one of them may be taken as the definition:

• For all g in G, gNg⁻¹ ⊆ N.
• For all g in G, gNg⁻¹ = N.
• The sets of left and right cosets of N in G coincide.
• For all g in G, gN = Ng.
• N is a union of conjugacy classes of G.
• There is some homomorphism on G for which N is the kernel.

The last condition accounts for some of the importance of normal subgroups; they are a way to internally classify all homomorphisms defined on a group. For example, a non-identity finite group is simple if and only if it is isomorphic to all of its non-identity homomorphic images, a finite group is perfect if and only if it has no normal subgroups of prime index, and a group is imperfect if and only if the derived subgroup is not supplemented by any proper normal subgroup.

Examples

• The subgroup {e} consisting of just the identity element of G and G itself are always normal subgroups of G. The former is called the trivial subgroup, and if these are the only normal subgroups, then G is said to be simple.
• The center of a group is a normal subgroup.
• The commutator subgroup is a normal subgroup.
• More generally, any characteristic subgroup is normal, since conjugation is always an automorphism.
• All subgroups N of an abelian group G are normal, because gN = Ng. A group that is not abelian but for which every subgroup is normal is called a Hamiltonian group.
• The translation group in any dimension is a normal subgroup of the Euclidean group; for example in 3D rotating, translating, and rotating back results in only translation; also reflecting, translating, and reflecting again results in only translation (a translation seen in a mirror looks like a translation, with a reflected translation vector). The translations by a given distance in any direction form a conjugacy class; the translation group is the union of those for all distances.
• In the Rubik's Cube group, the subgroup consisting of operations which only affect the corner pieces is normal, because no conjugate transformation can make such an operation affect an edge piece instead of a corner. By contrast, the subgroup consisting of turns of the top face only is not normal, because a conjugate transformation can move parts of the top face to the bottom and hence not all conjugates of elements of this subgroup are contained in the subgroup.

However ,evenif H is a normal subgroup of G ,this does not mean that ah=ha for all h€H and for all a€G.As the following example shows : Consider the group S3. Let H={e,(1 2 3),(1 3 2)}. Then H is a subgroup of S3. Since e,(1 2 3) and (1 3 2) are elements of H , it follows that eH=He ,(1 2 3)H=H(1 2 3) and (1 3 2)H=H(1 3 2) .Now (1 2)H={(1 2),(1 2)(1 2 3),(1 2)(1 3 2)} H(1 2)={(1 2),(1 3 2)(1 2),(1 2 3)(1 2)} Hence (1 2)H=H(1 2) (2 3)H={(2 3),(2 3)(1 2 3),(2 3)(1 3 2)}={(2 3),(1 3),(1 2)} H(2 3)={(2 3),(1 2 3)(2 3),(1 3 2)(2 3)}={(2 3),(1 2),(1 3)} Hence (2 3)H=H(2 3) Also in the same way this can be shown that (1 3)H=H(1 3) Consequently H is a normal subgroup.However we point out that for (1 2 3)€H and (2 3)€G(=S3) (2 3)(1 2 3)=(1 3)≠(1 2)=(1 2 3)(2 3)

Properties

• Normality is preserved upon surjective homomorphisms, and is also preserved upon taking inverse images.
• Normality is preserved on taking direct products
• A normal subgroup of a normal subgroup of a group need not be normal in the group. That is, normality is not a transitive relation. However, a characteristic subgroup of a normal subgroup is normal. Also, a normal subgroup of a central factor is normal. In particular, a normal subgroup of a direct factor is normal.
• Every subgroup of index 2 is normal. More generally, a subgroup H of finite index n in G contains a subgroup K normal in G and of index dividing n! called the normal core. In particular, if p is the smallest prime dividing the order of G, then every subgroup of index p is normal.

Lattice of normal subgroups

The normal subgroups of a group G form a lattice under subset inclusion with least element {e} and greatest element G. Given two normal subgroups N and M in G, meet is defined as

and join is defined as

The lattice is complete and modular.

Normal subgroups and homomorphisms

If N is normal subgroup, we can define a multiplication on cosets by

(a₁N)(a₂N) := (a₁a₂)N.

This turns the set of cosets into a group called the quotient group G/N. There is a natural homomorphism f : G → G/N given by f(a) = aN. The image f(N) consists only of the identity element of G/N, the coset eN = N.

In general, a group homomorphism f: G → H sends subgroups of G to subgroups of H. Also, the preimage of any subgroup of H is a subgroup of G. We call the preimage of the trivial group {e} in H the kernel of the homomorphism and denote it by ker(f). As it turns out, the kernel is always normal and the image f(G) of G is always isomorphic to G/ker(f) (the first isomorphism theorem). In fact, this correspondence is a bijection between the set of all quotient groups G/N of G and the set of all homomorphic images of G (up to isomorphism). It is also easy to see that the kernel of the quotient map, f: G → G/N, is N itself, so we have shown that the normal subgroups are precisely the kernels of homomorphisms with domain G.

See also

References

• I. N. Herstein, Topics in algebra. Second edition. Xerox College Publishing, Lexington, Mass.-Toronto, Ont., 1975. xi+388 pp.
• David S. Dummit; Richard M. Foote, Abstract algebra. Prentice Hall, Inc., Englewood Cliffs, NJ, 1991. pp. xiv, 658 ISBN 0-13-004771-6

External links

• Weisstein, Eric W., "normal subgroup" from MathWorld.
• Normal subgroup in Springer's Encyclopedia of Mathematics
• Robert Ash: Group Fundamentals in Abstract Algebra. The Basic Graduate Year
• John Baez, What's a Normal Subgroup?